可愛い顔した hero
お姫様じゃないの
強気で戦う
運命なんて変えてゆくわ
T2. SYOJ #1929
猫猫和矩阵(makrix)
是赛时手玩样例摸索出来的正解之外的新做法,正解是纯归纳法,我这个加了一点一个前缀和转换的思想,从某种意义上讲,这样好像更具象一些,愚蠢但有意思,就是实现略微麻烦点。
【大体思路】
前缀和 + 归纳法 + 单调栈
【详解】
首先先来观察题目中的式子:
移项以后得到:
感觉有点像二维前缀和?
顺着这个思路,画个图看一下:
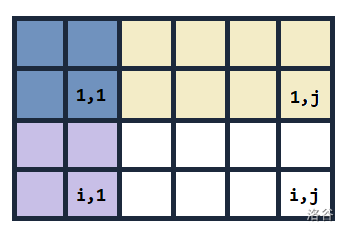
上面就是给出的矩阵,就把它看成一个前缀和数组。
取里面的一个子矩形 ,也就是从 到 这个矩形。首先我们知道,已知一个前缀和数组,我们可以逆推出它的原数组。
设由矩形 逆推得到的原数组是 数组,套进刚才我们推出的式子,可以得到:AC矩形 满足 整个 A 数组的和 <= A 中有颜色部分的和 这个结论。
换种说法,就是:若 A 中白色矩形之和 <= 0,则 是一个AC矩形。
一个AK矩形的所有子矩形都是AC矩形,所以通过归纳法就可以知道一个AK矩形 对应的 数组 除了第一行和第一列以外,剩余部分中的每个数一定都是非正数。这个归纳法的过程与老师上课讲解的正解的过程相同。
举两个例子:
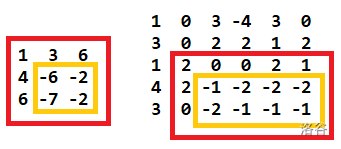
左侧是样例1推出的 数组,右侧是样例2推出的 数组。
红框内的就是 中最大的一个 “除第一行和第一列外其余位置都为非正数的矩形”,恰好就是它本身。
也就是说,我们现在只要找到 中最大的 “除第一行和第一列外剩下位置全负的矩形“,这道题就结束了。
这个问题用悬线法或是单调栈之类的解法都能做,但是用这种解法可能需要处理的细节会多一些,比如除去第一行和第一列的操作。
【代码】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 5;
int n, m, l[N][N], r[N][N], len[N][N], w[N];
int s[N], top, res, ans, a[N][N], b[N][N];
int main() {
scanf("%d%d", &n, &m);
ans = max(n, m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &b[i][j]);
a[i][j] = b[i][j] - (b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]);
if (a[i][j] <= 0 && j == 1) {
a[i][j] = 1;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] <= 0) {
if (a[i][j - 1] > 0) {
l[i][j] = j;
} else {
l[i][j] = l[i][j - 1];
}
} else {
l[i][j] = j;
}
}
r[i][m + 1] = m;
for (int j = m; j >= 1; j--) {
if (a[i][j] <= 0) {
if (a[i][j + 1] > 0) {
r[i][j] = j;
} else {
r[i][j] = r[i][j + 1];
}
} else {
r[i][j] = j;
}
}
}
for (int j = 1; j <= m; j++) {
for (int i = 2; i <= n; i++) {
len[i][j] = r[i][j] - l[i][j] + 1;
if (a[i][j] > 0) {
len[i][j] = 0;
}
}
}
for (int j = 1; j <= m; j++) {
top = 0, res = 0;
for (int i = 2; i <= n + 1; i++) {
if (len[i][j] > s[top]) {
s[++top] = len[i][j];
w[top] = 1;
} else {
int wid = 0;
while (s[top] > len[i][j]) {
wid += w[top];
res = max(res, (wid + 1) * (s[top] + 1));
top--;
}
s[++top] = len[i][j];
w[top] = wid + 1;
}
}
ans = max(ans, res);
}
printf("%d", ans);
return 0;
}
|

